SIR модель и её варианты
Факторы, обеспечивающие затухание сетевых эпидемий, можно оценить на модели, в которой сетевые узлы существуют в трех состояниях: уязвимом (S), зараженном (I) и невосприимчивом (R). S + I + R = N. Для начала предположим, что узлы оказываются неуязвимыми только после излечения от инфекции. Вводя постоянную среднюю скорость «иммунизации» в единицу времени g, получаем систему уравнений:

В этой модели существует пороговое условие для развития эпидемии. На участке возрастания i(t) производная di/dt должна быть больше 0. Поскольку s(t) непрерывно уменьшается за счет инфицированных машин, то получаем, что для начала эпидемии необходимо:
s(0) > g/b ? r (5)
К сожалению, это условие выполняется очень легко, поскольку g определяется запаздывающей человеческой реакцией и необходимостью загрузки громоздких «заплат», а b – постоянно улучшающимися техническими характеристиками сети и «доброй волей» злоумышленника (он может вставить небольшую паузу в цикл размножения, чтобы не создавать катастрофического трафика и слегка понизить скорость инфицирования). Доля же уязвимых узлов обычно очень велика. Поэтому практически всегда b на много порядков превосходит g. (К примеру, при моделировании эпидемии Code Red v2 в [25] согласие с реальными данными достигнуто при соотношении b/g ~106.)
В реальных условиях «иммунитет» посредством установки антивирусного ПО, межсетевых экранов и «заплат» приобретают не только инфицированные узлы (I), но и уязвимые (S). Предполагая, что средняя скорость иммунизации примерно одинакова для узлов обоих типов и равна (столь же малой) величине g, получим:

и условие развития эпидемии (5) сохраняется.
r(t) = 1 – exp(–gt), откуда вытекает, что при достаточно большом времени любую эпидемию теоретически можно вроде бы и преодолеть. Проблема заключается только в том, что это время может оказаться неприемлемо большим.
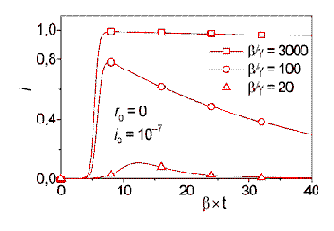
Рис. 3. Динамика развития эпидемии в системе (6) при сравнительно малой начальной зараженности сети (10–7). При b/g < 15 вспышка не происходит.
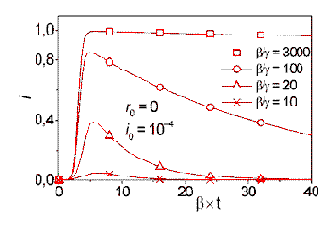
Рис. 4. Динамика развития эпидемии в системе (6) при значительной начальной зараженности сети (10–4). В этом случае пороговое значение b/g < 9.
Как видно из Рис. 3 и 4 при «вакцинации» уязвимых узлов для заметной эпидемической вспышки необходимо, чтобы скорость инфицирования превышала скорость иммунизации на два порядка и более, для того, чтобы за время порядка 1/g был пройден порог вспышки iпор. Пока что это не слишком обременительное условие для вирусописателей. Возможным выходом оказалась бы автоматизация процессов устранения уязвимостей. Она могла бы стать существенным фактором ограничения эпидемических рисков, конечно при условии, что черви не смогут блокировать систему обновления ОС, а сами автоматически устанавливаемые «заплаты» не будут нарушать работоспособность иммунизируемой системы и создавать в ней новые опасные уязвимости.
На практике же иммунизация незараженных узлов осуществляется гораздо медленнее, согласно принципу «пока гром не грянет». К тому же часть машин, на которых червь уничтожается, так и остаются «незалатанными», а при расширении Сети появляются новые узлы, «уязвимые» по умолчанию. Поэтому повторные эпидемические вспышки могут происходить с завидной регулярностью.
Динамика системы с переменным числом узлов будет определяться скоростью прироста новых уязвимых (S) узлов a:

Теперь условие развития эпидемии приобретает вид: s > (g + a)/b (8)
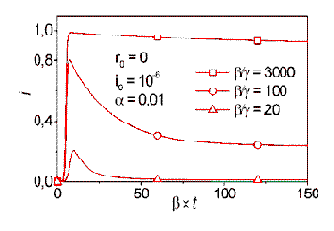
Рис. 5. Динамика развития эпидемии в системе (7).
Основной отличительной особенностью системы (7) оказывается наличие постоянного уровня, к которому со временем стремиться доля инфицированных компьютеров (Рис. 5 ). Это означает, что в реальных условиях от конкретного вируса в системе с приростом уязвимых узлов полностью избавиться нельзя даже при автоматической «вакцинации». Хотя бы и незначительное постоянное добавление новых уязвимых узлов создает «резервации», обеспечивающие повторные вспышки при благоприятных условиях.